I’ve just finished Geoff Hinton’s neural networks course on Coursera. It’s been considerably tougher than the other courses I’ve done there; Andrew Ng’s machine learning course and Dan Jurafsky & Chris Manning’s natural language processing course.
Whereas the other courses could serve as theory-light introduction for people who only have experience as coders, Hinton’s course expects basic understanding of probability and linear algebra and the ability to calculate non-trivial partial derivatives. There was a lot of supplementary material, including research papers and optional extra projects. I think I spent just a few hours on them, but I could have easily spent 20-30.
All of the above-mentioned people are leading researchers in their fields, and it’s pretty amazing that this material is available free of charge. This is something you just couldn’t get at eg. the University of Helsinki where I work. If you’re not familiar with Coursera, there are video lectures with mini-quizzes, reading material, more involved weekly exams, programming assignments and final quizzes, all nicely integrated.
You have to get at least a 80% score on each exam and assignment to pass, which is close to “mastery learning”, which I think is a good idea. This is in contrast to regular schools, where you might get a 50% score and then just keep moving on to more difficult material. To get mastery learning right, you have to allow exam retakes, which requires a large number of possible exams so that students can’t get a perfect score by just trial and error. This course didn’t completely achieve that, leaving it partly down to the student not to resort to trial and error.
By the way, don’t confuse mastery learning, which has to do with humans studying, with machine learning or deep learning, which are computational techniques to get computers to do things!
I’ve also attended a study group on the “Deep Learning Book” (henceforth DLB), and followed Andrej Karpathy’s lectures on convolutional neural networks (henceforth CNN) (which I think are no longer freely available because they didn’t have subtitles and so deaf people couldn’t watch them, so Stanford had to take them down – but I have copies). I’m going to do a little compare & contrast on these neural networks study resources. There is a lot of jargon, but at the end I’ll include an “everyman’s glossary” where I try to explain some concepts in case you’re interested in this stuff but don’t know what the things I’m talking about mean.
***
Hinton’s career has mostly been in the era of neural networks showing great promise but not quite working, and he tells you a lot about what hasn’t worked historically. Even things like backpropagation, which is used everywhere now, was developed and abandoned in the 80’s when people decided that it was never going to work properly. Other resources just tell you what works great, but leave out a lot of details about how careful you have to be to get things started the right way.
DLB is rather focused on feedforward nets and variations of them, all trained with backpropagation, and of course CNNs are the main feedforward model for anything having to do with visual data. Even recursive networks are presented as an extension of feedforward nets, which is not the way things developed historically.
Hinton presents a much more diverse cast of models, some of which were completely new to me, eg. echo state networks and sigmoid belief nets. Some of the time I was thinking “If this isn’t state-of-the-art, am I wasting my time?”, but ultimately all the material was interesting.
DLB and Karpathy made everything seem intuitive and “easy”, presenting a succession of models and architectures getting better and better results. Hinton made things seem more difficult and made you think about the mathematical details and properties of things much more. If you like engineering and results, go for DLB and the CNN course (and the Ng machine learning course first of all) – if you like maths, history and head-scratching, go for Hinton.
Hinton uses restricted Boltzmann machines (henceforth RBM) a lot. They are introduced via Hopfield nets and general Boltzmann machines, and used especially for unsupervised learning and pre-training. They are trained with something called contrastive divergence, an approximation technique that was new to me. Weight sharing is a recurring theme, used to develop intractable “ideal” models into practical models with similar characteristics. Dropout, which in DLB is just a normalization technique, is derived by Hinton as combining an exponential (in number of units and dropout) number of models with weight-sharing. ReLu units, which are introduced in DLB in an extremely hand-wavy way, are actually derived by Hinton as a limiting case of using multiple logistic units in parallel.
DLB and Karpathy mostly ignore the topic of weight initialization, saying that it’s no longer necessary. With Hinton it’s more central, probably because that was how the deep neural network revolution got really going originally. He points to architectures that were promising but didn’t work in the 80’s – 90’s but started working better with eg. RBM pretraining + backprop fine-tuning. Later he says that a stack of denoising or contractive autoencoders probably works even better for pretraining.
I found the pretraining methods interesting from a cognitive science standpoint. Denoising autoencoders lead to models where all the neurons are forced to model correlations between features, and RBMs & contractive autoencoders tend to lead to “small active sets”, where most of the hidden layer is insensitive to most inputs.
Hinton’s “final conclusion” about pretraining is that it will continue to be useful for situations where you have a smaller amount of labeled data and a larger amount of unlabeled data. With unsupervised pretraining you can still use the unlabeled data, which surely contains valuable information about the data space. That’s probably true, but I guess with images we now have enough labeled data.
The other problem for which pre-training is useful is very deep nets where the learning gradients vanish if you initialize all weights to be small random weights. I understand that this is now handled by directly connecting far-apart layers to each other, allowing information about the data flow both through deeper and shorter stacks of neurons.
Hinton reports that he’s had arguments with people from Google saying that they no longer need pretraining OR regularisation because they have such a huge amount of labeled data that they won’t overfit. Hinton argues that once they use even bigger and deeper networks they’ll start overfitting again, and will need regularisation and pretraining again, and I think that has happened (Hinton’s course is from 2013), at least for regularisation.
Hinton has some quite demanding programming exercises with little guidance, sometimes too little. Different regularisation methods are covered, including somewhat obsolete ones like early stopping, and you get a good overview of the differences. The exams are a mixed bag – many annoying underspecified questions with gotcha-answers, but also good mathy ones where you have to get a pencil and paper out.
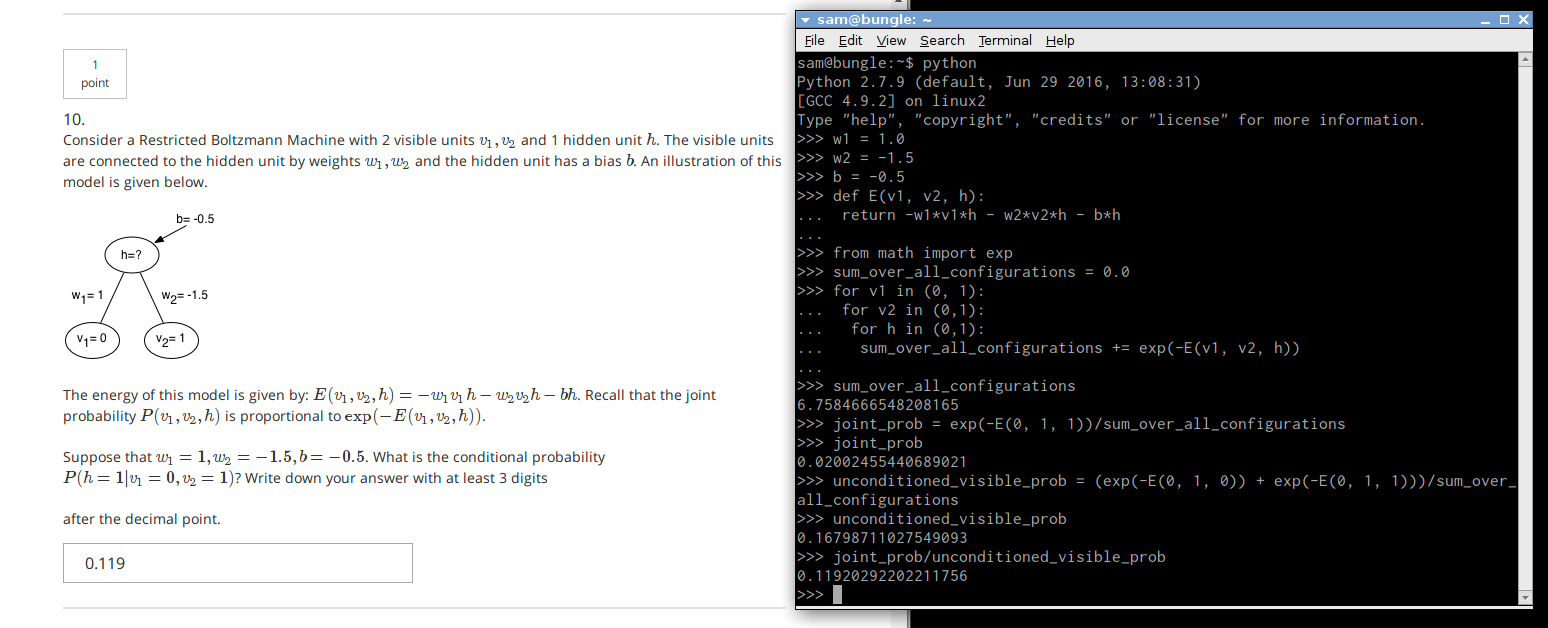
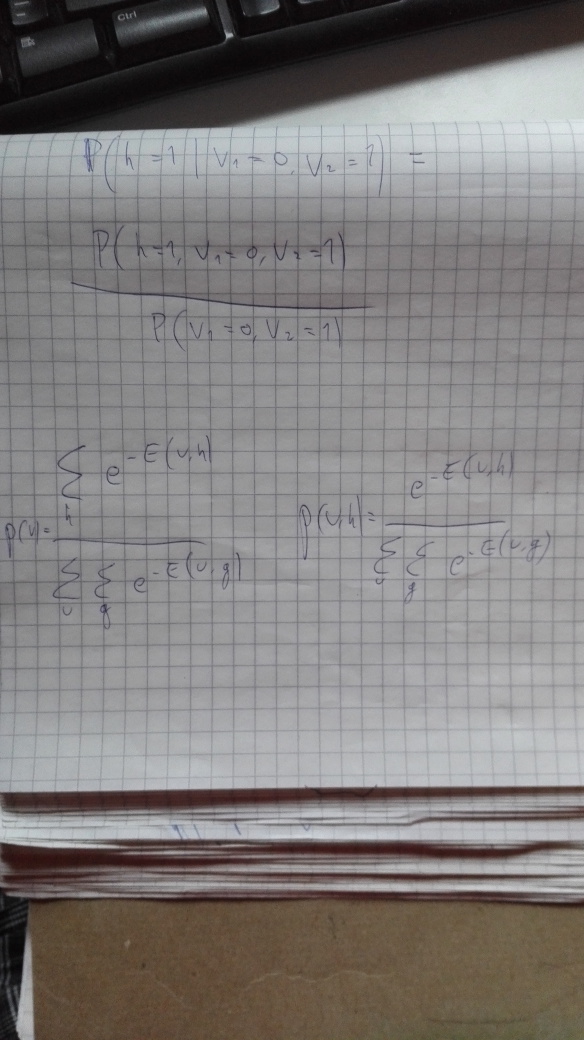
Here’s an example – it’s not really hard, but you have to think back quite far in the course and do some actual calculations. The screenshot shows the problem and the way I calculated the solution. The scribbles on the notepad show formulating the conditional probability that the question is about in terms of the probability of the joint configuration and the probability of just the visible units, and showing the probabilities of those in terms of the energy function E. Click to enlarge.
Whereas Hinton has quite a lot of emphasis on doing math by hand, rather than eg. just using software to handle everything via backprop, DLB is more oriented towards the engineering and applications side. Hinton has you not just calculating gradients, but deriving and proving properties of what learning does to the network etc.
Hinton does cover CNNs as well, but in a more theoretical way, not covering a litany of models and approaches. He shows AlexNet from 2012, and then later when covering image retrieval he first training a deep autoencoder to hash images into binary codes and uses Hamming distance to find matches. This works, but is a lot less impressive than the state of the art. Then he swaps out the image data his autoencoder is getting for the activations from AlexNet and gets a really good image retrieval system. A nice example of the development of the field.
***
An everyman’s glossary
Neural network: a system that connects individual units of very simple computation together in order to get the network of these units to accomplish some more complicated task. These systems are behind things like Google image search, self-driving cars and recommender systems that try to predict what you’re interested in buying next.
Objective function / loss function: a way to measure what you’re trying to achieve. Eg. if you’re trying to detect objects in pictures, the objective function measures how well your system did at detecting objects in pictures where the content is already known. This is called “supervised learning”.
Backpropagation: a way to determine for each part of the network what way it should change in order to better satisfy the objective function. This involves calculating the derivative of the objective function with respect to the parts immediately before the output layer, and then re-using those derivatives to calculate the derivatives for parts further along in the network. If you remember the “chain rule” from calculus in school, this is essentially doing that over and over again.
Feedforward net: a neural network architecture where the input data is one layer and influences neurons on the next layer, which influences the next layer etc. Each connection between neurons is a “weight”, which is a number used to multiply the activation from the output-neuron and fed into the input-neuron. The final layer is the “output layer”. No backwards connections. A model like this is usually learned by using backpropagation to compute gradients (how should we change the weight) from the objective function to each weight, and then optimizing the weights using that.
Deep net: this just means that there are multiple layers of “hidden neurons”, meaning units that aren’t part of the input or the output of the system. Training (ie. finding good weights) a net like this is “deep learning”.
Optimization: in the context of neural networks, a method for finding good weights for all the connections in the network, given the gradients of the objective function with respect to each connection. Some version of “gradient descent” is typical. This is changing all the weights a small step in the direction of their respective gradients, recalculating the gradients, taking another step etc. until the objective function doesn’t get any better anymore.
Activation function: this is what a neuron does to its inputs to determine its own activation. For example, linear activation is taking each input, multiplying it by a weight and adding all of those together. This is linear because it can just scale the previous activations to be bigger or smaller. Its graph is a straight line. Complicated problems require nonlinear activations, like the logistic function, which has an S-shaped graph.
Unsupervised learning: this is where you don’t have an objective function, but are just trying to understand the data in some way. This can be useful for pretraining deep supervised networks.
Pretraining: in deep nets, it is sometimes difficult to get training to work because the hidden layers can be many layers separated from the output layer, where the objective function is calculated. In pretraining you first train the hidden layers separately to model the previous layer well (in an unsupervised way, without caring about the objective function), and then finally you stack them together and use backpropagation to fine-tune the system with the objective function.
ReLu / rectified linear unit: the simplest kind of nonlinear activation function. When the input is negative, it outputs zero, and when the input is positive, it outputs the input. The graph is two straight lines put together, with one point of nonlinearity (and noncontinuity). Very commonly used today.
RBM / Restricted Boltzmann Machine: an undirected neural network, where connections between neurons are two-way (but with just one weight covering both directions), and the whole system is made to minimize an “energy function”, making the configurations of the whole system conditional on the given data simple and probable. The “restricted” part means that there are no connections between hidden units, just between the inputs and the hidden units.
Underfitting / overfitting: underfitting is when the system is unable to model structure in the data because it doesn’t have enough modeling capacity. Overfitting is when the system has so much capacity it models even random correlations in the data, leading to bad performance when new data doesn’t have those random correlations. This is remedied by using regularisation techniques, like adding terms to the objective function making the network want to be simpler and more generalising.
Autoencoder: a system that uses an input to reproduce itself via some simpler intermediate representation. For example, taking 256-by-256 pixel images, encoding them into a vector of 20 numbers, and trying to use that encoding to reproduce the original image as well as possible.
Tell me if I’m missing something important from the glossary.