The paper today had a look into the cost of family-sized pizzas in Helsinki. The story found that family-sized pizzas are a rip because the cost per area was greater than in the normal ones. Whoa! Though I wonder why they didn’t weigh the pizzas.
It occurred to me that the reporter had made the assumption that pizzas grow proportionally, ie. that the crust is as much bigger in a big pizza as the radius. I don’t think this is true – the crust is closer to being constant in width. If this is so, the topping part of the pizza grows quadratically while the crust grows constantly, so some of the extra value of the big pizzas is being overlooked in the newspaper story: with r the radius of the pizza and c the width of the crust, the area of the crust is
pi*r2 – pi*(r-c)2 = pi*(r2 – r2 + 2*c*r – c2) = pi*2*c*r – pi*c2 = A*r + B
where A and B are constants. How significant is this oversight? Pretty significant:
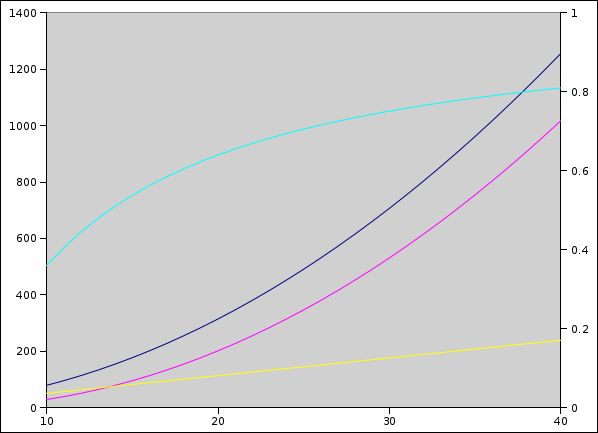
Here the dark blue line is pizza surface area, magenta is topping surface area, and yellow is crust surface area (left scale, cm2). Turquoise is the ratio of topping to pizza (right scale, from 0 to 1). The x-axis represents diameter of pizza in cm. A crust width of 2 cm is presumed throughout. Over the pertinent range, 30 to 40 cm in diameter we go from 75% topping to 80% topping. The marginal topping ratio (the topping ratio of just this extra bit of pizza) of this growth is a whopping 89%! Too bad they don’t sell marginal pizza. Also, I actually rather like the crust.
Still, IS THIS WHAT THEY CALL JOURNALISM THESE DAYS HUFF BHURR

I’ve had plenty of pizzas that were marginal at best ;)
Wonderfully nerdy analysis. I was all ready to chide you for assuming that the crust was an inferior part of the pizza until I got to the end…
Jason