Not a great week for pictures.
First, I don’t want to give the impression that I’m all about trying to sketch real-world objects, so here’s a piece of creativity from deep within my soul. I call it “Gretel is affected by a mushroom and vomits out his soul”:
I consider weeks to begin on Mondays, so this is for the first two days of the year.
I immediately went back on what I said about not attempting difficult things like shading, and started doing a really ridiculously over-difficult study of a paper-covered vase and an amaryllis plant in it.
I could spend ten hours doing this kind of texture and not get it right. As it was, I spent about an hour. The vase part was sketched with a light sepia pencil, with some highlights in a white pastel one. I used a paper stump to get some of the smoother shading parts. The red ribbon I did with a stick of burnt sienna (which is not intended for detailing, but it’s what I had). There’s some graphite pencil in the outlines as well. I started doing the colour for the plant with a set of waxy sort of pencils (quite old ones my wife had gotten at some point), but didn’t like them much. Very difficult to get good coverage or shading, plus you’re completely stuck with the colours in the set. The green parts are in the wax colour, as are the left-and rightmost red leaves and yellow anthers. I then gave up on the wax and finished up in disgust with my trusty watercolour set (six incredibly well chosen colours).
At the very beginning I tried to get “all” the detail in, but once I realised there was just no way, I settled for getting a right-ish impression. Here’s a photo of the plant – the lighting’s not quite right and the orientation is a bit different here, but you get an idea of my degree of fidelity:
Another problem of mine is using space: not only did I end up cutting off half the flower, I’d made the vase so big and detailed that the flower had to be rather smaller than life to fit in at all. I should have made it a natural size, draw only the very bottom and make the picture be more about the vase (although that was my main interest anyway).
Here’s a gel pen rendition / sketch of my pocketknife / multitool thing.
Not much to say, really. You can again see that I ran out of space. This sort of thing I could do a bit better by just spending more time on it and being careful, but for now I want to do things fairly quickly and just get used to drawing. Anyway, it’s not that bad in a cartoony way.
Inspired by tjic, a somewhat strange bedfellow, I’ve uncharacteristically decided to set myself a goal/resolution for 2011. I’ve set my sights a good deal lower than that fellow’s overcome-everything mindset (make money, build things, lose weight, learn instrument), but I’ll nevertheless be happy if I succeed. Heck, knowing me, I’ll most likely be happy even if I don’t! The goal is to make and publicly display 6 pictures a week for all of 2011. “Display” means “post here”, obviously. Turn off your RSS readers, gentlemen! I will probably do a post a week with the whole bunch. I hope to draw considerably more than 6 a week, but that’s what I aim to dare show and be bothered to scan and upload.
6 is probably more than I’ve done in a whole year most years. At the age of around 14-15 I had a period of sketching a fair bit, and again around 16-17 (I’m 25 now), so I’m very unpracticed and shoddy. In the latter part of 2010 I did some quick watercolours. But I do like drawing, a lot, and I hope this will improve my skill and make it even more fun. Perhaps more importantly, it would also be nice to get a habit of openness and willingness to reveal weaknesses in order to improve them.
My greatest weaknesses in drawing currently are probably in shading, perspective (I can’t think spatially for shit) and patience. I’ll probably start out by not attempting those, and attack them with more practice later.
Before I move on to show-and-tell, an anecdote about spatial thinking. This Thursday I was thinking about this Project Euler problem (by the way, skip this paragraph if you don’t want to be spoiled vis-a-vis the problem). I wanted to figure out a way to determine the shortest path from one corner of a cuboid to the direct opposite, using only the sides (if you prefer: in a room whose ceiling, floor and walls are rectangles, the shortest path for an ant to crawl from a corner on the floor to the opposite corner on the ceiling). My first idea was to find a suitable variable and differentiate: have the ant travel along the floor to some point x on the edge between the floor and an opposite wall, and then along the wall directly to the corner. x now determines the length of the path, so differentiate and find the zero of that function, and there you have it. Of course there are other ways to choose the path as well, so for each you have to derive the appropriate functions and do the same thing, and find the minimum from all those possibilities. The manipulations become rather hairy and fiddly… In a bar that evening I mentioned this to someone who almost immediately suggested that I could just fold the cuboid open and draw the paths as direct lines. Like this:
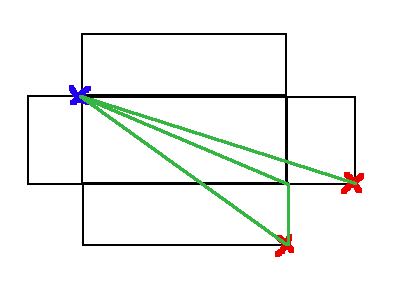
The blue cross is the starting point, the red crosses are points that map to the target corner, the three green paths are the possible minimal ones (except that with this diagram you can immediately see that it's never best to go across to a corner and straight up because it isn't a straight line).
It’s all right triangles, easy peasy. This was so simple it took me a while to accept that this was really correct! This is what I mean by terrible spatial thinking ability.
Anyway. To give you some idea of where I am, here’s a bunch of recent sketches.
An impression of a table with a seated figure. The blue overhanging thing is a lamp.
A quick bar sketch
Another quick bar sketch. The mess on the forehead is a failed attempt at an eye. On the chin is not a beard, but another false start.
What prolonged drinking will do:
An impression of six people at a table (from my perspective, I was sitting at the head of the table - squint hard, you'll see it eventually)
My first attempt at a transvestite - not sure what I was thinking here
For Finnish readers, a bonus: a selection of rather puzzling children’s stories with illustrations I wrote when I was 14 or so.
The fireplace started smoking out of its right side. There’s a brick wall that’s supposed to meet the mantel and keep the smoke in, but it has started leaning in, letting the smoke out. In fact all the brick lining, especially in the back, is beyond its useful lifespan and failing.
Note leaning right wall
rss2 feedThey say the unexamined life isn’t worth living. I examined my life, and turns out it still isn’t worth living.