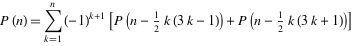In the proud tradition of this blog I’m holding a new smallest number tournament. The rules of this wonderful game are as follows:

1. Each player chooses an integer greater than zero.
2. If more than one player chooses the same number, that number is disqualified.
3. The player who played the smallest number that didn’t get disqualified wins.

For example, if Bernie plays 1, Joan plays 2 and Dave plays 5, Bernie wins, because he played the smallest number. But if there had been an extra participant, Frank, who had also played 1, Joan would have won, because 1 would have been disqualified and 2 was the next smallest number played.

But this time I don’t want you to play the game – I want you to write a small program that plays the game. There are two ways to participate in this contest

Firstly, you can write a Python class that has at least the following methods (all of these except play() can just pass):

• announce_num_players(integer): take an integer giving the number of participants in the tournament, don’t return anything
• announce_game_length(integer): take an integer giving the number of rounds that will be played, don’t return anything
• get_ready(): do any final initialization
• announce_result(result): take a list with all the other players’ plays from the most recent round (the same player will always occupy the same place in this list)
• play(): return your number for the round

An example minimal contestant could look like this:

class Player:
    def __init__(self, number = 4):
        self.always_play_this_number = number
    def get_ready(self):
        pass
    def announce_num_players(self, num):
        pass
    def announce_game_length(self, num):
        pass
    def announce_result(self, result):
        pass
    def play(self):
        return self.always_play_this_number

(Always play 4 unless initialized to always play something else, and don’t do anything with the extra information.)

Secondly, you can come up with a distribution. It can be a constant distribution, with constant probabilities for each number, like this:

[0.3, 0.3, 0.3, 0.1]

(play numbers 1-3 with a probability of 30% each and number 4 with a probability of 10%)

or a list comprehension that uses information about the number of players and rounds, like this:

[1.0/num_players for x in range(num_players)]

(play numbers up to the number of players with equal probability)

or any other convenient-to-me way of describing a distribution in list form.

Submissions are open until I’m satisfied that most people I know who might be interested have had time to come up with a submission. I will be happy to help with the programming if you’d like. I will be participating myself, but I promise I will not use information from other submissions.

Send submissions to my email address which should be visible in the side panel, preferably with a subject like “Smallest number challenge”.

The prize is the joy of participation, and it will be given to all participants!

Details about the tournament arrangements

I will score each tournament in at least two ways: the official way and Vadim’s zero-sum way.

• In the official scoring, a player who plays a winning move receives one point. A player who doesn’t play a winning move receives zero points.
• In Vadim’s zero-sum scoring for n-player tournaments, the winner gets n-1 points, losers get -1 point, and if there’s no winner, everyone gets 0 points.

I will run several tournaments with varying numbers of rounds, all with the full complement of participating players.

The tournament-running program will always call announce_game_length() and announce_num_players() for each player before a tournament starts, and announce_result() every time a round has been completed. Players that support the special value None as an argument from these functions will participate in a special tournament where the players don’t get this information.

Programming used to have a lot to do with little puzzles and tricks; pointer arithmetic, bitmasks and logical operators, writing to video memory etc. Someone once asked me how do you swap the contents of two (numerical) variables without using a third one in between (of course you’d never want to do this anyway, but it’s a “fun” question). The answer is something like this:

a = a+b
b = b-a
a = a+b
b = -1*b

This is how you do it in Python:

a, b = b, a

New-fangled programming languages, eh? (Ok, Python was first released in 1991 which was a long time before I programmed anything, but anyway.)

Apropos of that last notation, this is how you write Euclid’s algorithm in Python (% is the modulo operator):

def euclid(a,b):
        while b:
                a, b = b, a%b
        return a

It’s sickeningly succinct, really. I kind of quite like it, but it kind of feels not very hardcore (comparing to, say, The Story of Mel which I’ve linked to before). Although really it’s just normality by now. Meh, meh.

What makes a man turn neutral? Lust for gold? Power? Or were you just born with a heart full of neutrality?

>>> True or False
True
>>> True and False
False
>>> True = False
>>> not True or False
True
>>> not not not not not not False
False
>>> True/False
Traceback (most recent call last):
File “<stdin>”, line 1, in
ZeroDivisionError: integer division or modulo by zero