Millä tahansa ohjelmointikielellä voi tehdä mitä tahansa. Joillain ohjelmointikielillä voi “yleensä ottaen” ilmaista asiat lyhyemmin tai luonnollisemmin kuin joillain toisilla, mutta useimmilla kielillä on jokin omin alueensa jota varten ne alunperin suunniteltiin, ja tällä kotikentällä on niiden kanssa paljon luontevampaa toimia kuin muilla kielillä.
Olen viime vuosina silloin tällöin yrittänyt perehtyä Lisp-ohjelmointikieleen (tai oikeammin sen moniin variantteihin), koska gurut mielellään kehuvat sen tajuntaa laajentavia ominaisuuksia. Lisp on eräs kaikkein vanhimpia ohjelmointikieliä, mutta tästä huolimatta se on eräs kaikkein ilmaisuvoimaisimmista. Useimmissa ohjelmointikielissä koodi annetaan kääntäjälle tai komentotulkille joka jäsentää sitä syntaksipuiksi ja generoi puista konekieltä tai muuten suorittaa sen komennot. Lispissä mitään jäsennysvaihetta ei ole, vaan koodi kirjoitetaan valmiiksi jäsennettynä.
Konkreettisesti: sen sijaan että käytettäisiin ohjelmointikielen syntaktisia apuneuvoja – silmukkarakenteita, erityismerkintöjä erilaisille tietorakenteille ja niin edelleen (jotka ohjelmointikielen kääntäjä sitten tulkitsee) kirjoitetaan suoraan syntaksipuita sellaisenaan. Tästä seuraa erilaisia mystisiä asioita, joista monet liittyvät siihen että on helppoa kirjoittaa koodia joka generoi tai muokkaa näitä syntaksipuita, jolloin ohjelmoija ei ainoastaan ohjelmoi ohjelmaansa vaan koko ohjelmointikieltä.
Syystä tai toisesta Lisp ja sen perilliset eivät kuitenkaan ole kovin yleisessä käytössä. Ohjelmoijat kaipaavat jotain tukea yleisesti tarvittuihin operaatioihin. Lisp-koodi näyttää kaikkialla aika samalta, siellä ei ole visuaalisia merkkejä jotka sanovat että tässä on taulukko[], tässä funktio() ja tässä silmukka:
for asia in kokoelma:
prosessoi(asia)
Olen kuitenkin uskollisesti perehtynyt Lispin saloihin, lueskellut kirjoja, tehnyt harjoituksia ja pohdiskellut. Vasta muutama päivä sitten tuli vastaan tilanne, jossa halusin tehdä jotain joka ilmiselvästi kuului tehdä Lispillä. Valitettavasti tämäkään ei ollut “oikea” tarve, vaan eräs ohjelmointipähkinä. Jaan sen kuitenkin kanssanne antaakseni pienen fleivörin siitä, millaisia asioita Lispillä on erityisen kätevä tehdä. Kyseinen pähkinä on Project Eulerin tehtävä numero 93. Vapaasti suomennettuna tehtävä on seuraavanlainen:
Käyttämällä kutakin luvuista 1, 2, 3 ja 4 täsmälleen yhden kerran ja lisäämällä aritmeettisia operaatioita (+, -, *, /) ja sulkeita on mahdollista muodostaa muita kokonaislukuja.
Esimerkiksi,
8 = (4 * (1 + 3)) / 2
14 = 4 * (3 + 1 / 2)
19 = 4 * (2 + 3) − 1
36 = 3 * 4 * (2 + 1)Tässä lukujen kirjoittaminen peräkkäin, esimerkiksi 12 + 34, ei ole sallittua.
Käyttämällä joukkoa {1, 2, 3, 4} voidaan muodostaa 31 eri kokonaislukua joista 36 on suurin. Kukin luvuista 1 – 28 voidaan muodostaa tällä tavalla ennen kuin kohdataan ensimmäinen luku jota ei voida muodostaa (29).
Mitkä neljä yksinumeroista lukua voivat muodostaa pisimmän jonon kokonaislukuja alkaen ykkösestä?
Aluksi tuntuu siltä että kaikkia mahdollisia lausekkeita on aika monimutkaista rakentaa. Pitäisi käydä läpi kaikki eri tavat asetella sulkeita. Helpompaa on ehkä luetella kaikki mahdolliset tällaisten lausekkeiden jäsennyspuut (joka on oleellisesti sama asia). Esimerkiksi lausekkeen (3 – 1) * (7 / 2) jäsennyspuu on tällainen:
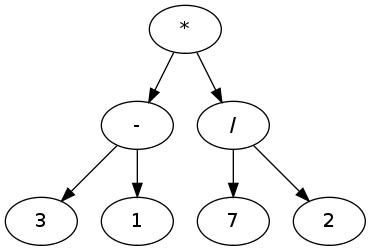
Jäsennyspuissa ei tarvita sulkeita, sillä operaatioiden järjestys on suoraan koodattu puun rakenteeseen. Niissä puissa joista nyt puhumme on operaattoreita, joilla on aina kaksi jälkeläistä, ja lukuja, joilla ei ole jälkeläisiä (ne ovat lehtiä). Tässä kertolaskun * jälkeläiset ovat molemmat puita. Ennen kuin kertolaskun tulos voidaan laskea, pitää laskea näiden puiden arvo. Ne ovat 3 – 1 (eli 2) ja 7 / 2. Sitten voidaan laskea kertolasku, joka on siis 2 * (7 / 2), jonka tulos on 7.
Lispissä kyseinen jäsennyspuu kirjoitetaan näin: (* (- 3 1) (/ 7 2)). Ensimmäisenä sulkeiden sisällä on puun (tai alipuun) juuri, jonka jälkeen luetellaan jälkeläiset.
Onneksi erilaisia nämä ehdot täyttäviä puita on vain viisi:
(op (op (op n n) n) n)
(op (op n (op n n)) n)
(op (op n n) (op n n))
(op n (op (op n n) n))
(op n (op n (op n n)))
Tässä op on laskutoimitus ja n on jokin luku. Ensimmäinen näistä puista näyttää tältä:
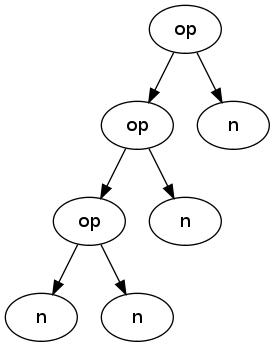
En näytä koko ratkaisua tehtävään, mutta esittelen sen erään keskeisen osan: Scheme-funktion (Scheme on käyttämäni Lisp-variantti – tarkemmin sanottuna käytän Scheme-varianttia jonka nimi on Chicken Scheme) jolle annetaan 4 lukua, esimerkiksi {3,5,7,9} ja jokin toinen luku, esimerkiksi 17, ja joka kertoo, voidaanko toinen luku muodostaa laskutoimituksilla mainituista neljästä luvusta.
Alkukehikko näyttää tällaiselta:
(define (canmake operands target) (let ((trees '( (op (op (op n n) n) n) (op (op n (op n n)) n) (op (op n n) (op n n)) (op n (op (op n n) n)) (op n (op n (op n n))) ))))) |
define määrittelee funktion nimeltä canmake, jolla on kaksi argumenttia: operands (luvut joista lauseke koostetaan) ja target (luku jota yritetään muodostaa). Funktiossa ei toistaiseksi tapahdu muuta kuin määritellään ympäristö (let (... jossa muuttujaan tree on sidottu lista aiemmin luettelemistani sallituista jäsennyspuista.
Seuraavaksi tarvitsemme luettelon mahdollisista laskutoimituksesta. Puussa on aina 3 operaattoria. Käytetään funktiota n-combinations joka muodostaa luettelosta asioita niiden mahdollisia yhdistelmiä. Se toimii seuraavasti (seuraava koodinpätkä suoritetaan interaktiivisesti jotta näkisimme mitä se tekee, “>” on rivi jolle kirjoitamme koodia ja loput on koodin suorittamisen lopputulos):
> (n-combinations '(* / + -) 2) ((- -) (+ -) (/ -) (* -) (- +) (+ +) (/ +) (* +) (- /) (+ /) (/ /) (* /) (- *) (+ *) (/ *) (* *)) |
Sille siis kerrotaan alkioiden luettelo '(* / + -) ja se miten monta kappaletta valitaan, tässä 2 (oikeasti haluamme 3 operaattoria, mutta niiden lista olisi turhan pitkä). Tässä operaattorit *, /, + ja - eivät ole vapaita muuttujia tai merkkijonoja, vaan Schemen sisäänrakennettuja laskutoimitusoperaatioita (tai tarkemmin sanottuna symboleja joihin nuo operaatiot on sidottu). Voimme siis vapaasti käyttää näitä operaattoreita luetteloissa.
Nyt funktiomme näyttää tältä:
(define (canmake operands target) (let ((ops (n-combinations '(+ * / -) 3)) (trees '( (op (op (op n n) n) n) (op (op n (op n n)) n) (op (op n n) (op n n)) (op n (op (op n n) n)) (op n (op n (op n n))) ))))) |
Nyt olemme lisäksi sitoneet symboliin ops kaikki mahdolliset kolmen operaattorin yhdistelmät. Kullekin tällaiselle yhdistelmälle voimme nyt testata, saammeko haluamamme lopputuloksen. Esimerkiksi luettelon ensimmäiselle ja puulle ja ensimmäiselle laskutoimituskolmikolle seuraavasti:
(= (eval(relabel (first trees) (first ops) operands)) target) |
Tässä relabel on funktio, joka ottaa argumenteiksi puun, operaattorilistan ja listan lukuja (operands) ja palauttaa puun jossa op ja n -symbolien tilalla on oikeat laskutoimitukset ja numerot. eval on sisäänrakennettu funktio joka evaluoi puun. Missä mielessä evaluoi? Lisp-mielessä! Puu (* (- 3 1) (/ 7 2)) ei ole lausekepuu vain meidän kannaltamme, vaan myös Lispin kannalta. Se on sellaisenaan suorittuvaa koodia, ja eval suorittaa sen ja palauttaa vastauksen. first palauttaa aina listan ensimmäisen alkion, ja target on se lopputulos johon yritettiin päästä. Pelkistettynä siis (= laskutoimitus target), eli testaamme yhtäsuuruutta muodostamamme lausekkeen ja targetin välillä. Jos ne ovat yhtäsuuria, tämä koodinpätkä evaluoituu todeksi (Schemessä #t), ja muuten epätodeksi (#f). Esimerkiksi (jälleen sessio komentotulkin kanssa):
> (relabel '(op (op n n) (op n n)) '(* - /) '(3 1 7 2))
(* (- 3 1) (/ 7 2))
> (eval(relabel '(op (op n n) (op n n)) '(* - /) '(3 1 7 2)))
7
> (= (eval(relabel '(op (op n n) (op n n)) '(* - /) '(3 1 7 2))) 7)
#t
Tässä vaiheessa tulee mieleen eräs pulma: miten evaluoidaan puu
(* 3 (/ 7 (- 3 3)))?
(- 3 3) on 0, joten tulemme tehneeksi jakolaskun nollalla. Se ei ole hyvä juttu:
> (eval(relabel '(op n (op n (op n n))) '(* / -) '(3 7 3 3)))
Error: (/) division by zero
Call history:
Korvataanpa eval omalla pienellä myeval-funktiollamme, joka huomaa nollalla jakamiset ja palauttaa sellaisen sattuessa arvon 0.
Kun mahdollisia puita on niin vähän (viisi kappaletta), voimme testata niitä kaikkia samaan aikaan seuraavalla hieman epäelegantilla tavalla (joka on kuitenkin helpoin ymmärtää):
((or (= (myeval(relabel (first trees) (car ops) operands)) target) (= (myeval(relabel (second trees) (car ops) operands)) target) (= (myeval(relabel (third trees) (car ops) operands)) target) (= (myeval(relabel (fourth trees) (car ops) operands)) target) (= (myeval(relabel (fifth trees) (car ops) operands)) target)) #t) |
or palauttaa arvon #t eli tosi, jos mikään luetelluista vertailuista on tosi. Vielä pitäisi käydä läpi kaikki laskutoimitusyhdistelmät. Tehdään se pienellä rekursiivisella apufunktiolla: se testaa aina luettelon ensimmäistä laskutoimitusyhdistelmää, ja jos se toimii, funktio vastaa myöntävästi. Jos ei toimi, funktio kutsuu itseään listan loppuosalla. Jos lista tyhjenee eikä mikään laskutoimitusyhdistelmä toimi, funktio palauttaa epätoden eli #f. Tähän tapaan:
(define (canmake-helper ops) (cond ((null? ops) #f) ((or (= (myeval(relabel (first trees) (car ops) operands)) target) (= (myeval(relabel (second trees) (car ops) operands)) target) (= (myeval(relabel (third trees) (car ops) operands)) target) (= (myeval(relabel (fourth trees) (car ops) operands)) target) (= (myeval(relabel (fifth trees) (car ops) operands)) target)) #t) (else (canmake-helper (rest ops))))) |
cond on konditionaalirakenne, joka testaa ensin, onko lista ops jo tyhjentynyt. Jos se on, palautetaan #f. Muuten testataan viittä mahdollista puuta. Jos jollain saadaan oikea lopputulos, palautetaan #t. Muuten kutsutaan funktiota uudelleen lopuilla laskutoimituksilla.
Vielä pitää kutsua tätä apufunktiota alkuarvolla joka vastaa koko laskutoimituslistaa. Lopputulos on tällainen:
(define (canmake operands target) (let ((ops (n-combinations '(+ * / -) 3)) (trees '( (op (op (op n n) n) n) (op (op n (op n n)) n) (op (op n n) (op n n)) (op n (op (op n n) n)) (op n (op n (op n n))) ))) (define (canmake-helper ops) (cond ((null? ops) #f) ((or (= (myeval(relabel (first trees) (first ops) operands)) target) (= (myeval(relabel (second trees) (first ops) operands)) target) (= (myeval(relabel (third trees) (first ops) operands)) target) (= (myeval(relabel (fourth trees) (first ops) operands)) target) (= (myeval(relabel (fifth trees) (first ops) operands)) target)) #t) (else (canmake-helper (rest ops))))) (canmake-helper ops))) |
Käsin tehdyn luetteloinnin lisäksi funktiossa on vain muutama rivi koodia, ja ennen kaikkea koodi on varsin yksinkertaista. Tämä on selvästi Lispin kotikenttää. Harjoitus lukijalle: käsin luetteloimisen sijaan generoi mahdolliset puut. Parametrisoi laskutoimitusten ja lukujen määrä.
