I had to bang my head against the keyboard for a long time to get through problem #76 at Project Euler. It’s a deceptively “easy” problem: In how many ways can you write 100 as the sum of at least two positive integers, disregarding different ways to order the summands? (Writing integers as a sum of positive integers is known as partitioning.)
For example, 7 =
6 + 1 =
5 + 2 =
4 + 3 =
5 + 1 + 1 =
4 + 2 + 1 =
3 + 3 + 1 =
4 + 2 + 2 =
4 + 1 + 1 + 1 =
3 + 2 + 1 + 1 =
2 + 2 + 2 + 1 =
3 + 1 + 1 + 1 + 1 =
2 + 2 + 1 + 1 + 1 =
2 + 1 + 1 + 1 + 1 + 1 =
1 + 1 + 1 + 1 + 1 + 1 + 1
so there are 14 ways, not counting writing it as 7.
100 is such a small number that I figured even a stupid solution would work, but my first naive method of overgenerating sums and throwing them all into a set was too slow (it was ok up to partitioning about 15, but 20 took over a minute already). I was sure early on that some sort of recursive solution would work, but I must have had a stupid day because it took me ages to hit on a suitable idea (recurse by partioning the greatest summand into two partitions every way possible until you get to a sum of ones). The forum for discussing the solution was quite interesting; many people had thought of cleverer dynamic algorithms, finding the solution in a couple of hundredths of a second. But it turns out that there’s a lot of real number theory behind this as well. There’s a good article on MathWorld. I think the “simplest” formula people used to get solutions in something like a millisecond was this recurrence relation:
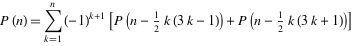
which apparently comes from a generating function using a q-series, discovered by Euler. I don’t really know what that means.
