I bought two books on my recent trip to New York: one about how large programming projects always fail (which I suggestively lent to my supervisor at work) and a collection of problems from mathematics olympiads in the Soviet Union. The latter included as commentary to one of the problems something a little surprising. First, the result:
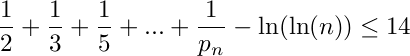
Where n is a natural number greater than 1 and pn is the nth prime. In other words, the sum of the reciprocals of the primes is approximated by ln(ln(n)) (natural logarithm) absolutely well, so that the difference never exceeds a constant (which is at most 14).
(The original problem was to prove that the sum of the reciprocals of the primes becomes arbitrarily large).
The distribution of primes among the natural numbers has interested mathematicians pretty much as long as mathematics has existed. One important result along these lines is the prime number theorem which states that the number of primes below n is approximately n/ln(n) in the sense that the relative error approaches zero (or their ratio approaches 1) as n increases. The absolute error (the difference, which is what the surprising fact is about), however, is (I think) not even known to be bounded. This is not at all easy to prove, and in fact it was only in 1896 that some people using non-elementary methods succeeded (this after Gauss had taken a swing at it).
I once attended a course named after this theorem, and the general feeling I got from it was that the distribution of primes is highly intractable and it’s difficult to prove even quite general things about it. Why should it then be that we can say something so precise about the sum of the reciprocals? The fact that this result was new to me implies that there’s some obvious reason why something like this is easier and less important.

Miten muuten sait noin ison kaavan näkyviin?
vadim
>The absolute error (the difference, which is what the surprising fact is
> about), however, is (I think) not even known to be bounded.
I am not sure what you mean. phi(n) – n/ln(n) approaches zero, this implies that phi(n) – n/ln(n) is bounded… what is the distinction between absolute and relative error?
vadim
Ahh, sorry for the previous nonsense. phi(n) – n/ln(n) does not approach zero necessarily
vadim
Voi olla et käytin jotain web-palvelua tai mahdollisesti yhtä nyt kadottamaani skriptiä joka teki sen latexin ja erinäisten komentorivikalujen kanssa.
sam
Siis semmosta jolle annetaan latexia ja joka tuottaa halutun kokoisia kuvia. Semmosia löytyy googlaamalla, tyyliin http://hausheer.osola.com/latex2png
sam
ai, ku mä käytän wordpressin LatexRender pluginia, joka tuottaa vakiokokoisia kaavoja. Kiitos.
vadim
vadim
Joo, mäkin varmaan käyttäisin jotain sellaista jos tekisin tommosta enemmän, kuvien kanssa pelaaminen on aika epäkätevää. Tosin voishan sitä varten tehdä oman skriptin/plugininkin…
sam
I started to wonder, should there be |absolute value| signs? So that it is not only less than 14, but also greater than -14..?
Vadim
I don’t know, maybe. I don’t think the book I got this out of did, although I changed the equation I got from it a bit to make it neater. Who knows, maybe the joke is that the error isn’t bounded below… I wonder how long a program would have to run to get some idea.
sam