The programming problems on Project Euler are almost always fun to do, but the mathematics behind the (early) ones have mostly been unsurprising. But this was something I hadn’t heard about: if you arrange the natural numbers in a counterclockwise square spiral and look at the diagonals like this
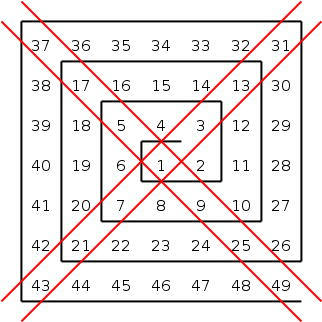
you notice that
1) the odd squares are on the lower right diagonal (easily proved and not so shocking)
2) 8 of the 13 numbers (~62%) on the diagonals in this 7×7 square are primes.
If you keep extending the spiral you find that primes end up on the diagonals surprisingly often. The programming task was to find what size the spiral has to be for the proportion of primes on the diagonals to be less than 10%. The suprisingly large answer: 26241×26241, by which point the numbers in question are obviously already quite big.
And of course if one discounted the lower right diagonal there’d be way more primes yet.
edit: apparently this is called the Ulam spiral.
